Chapter 10.3 - Gram Molecular Mass

In the previous section, we saw that 18 grams of water will give water molecules. In this section we will see two more examples like that:

■ Consider a molecule of carbon dioxide (CO₂). How many grams of carbon dioxide should we take so that, there will be N_A molecules of CO₂?
Solution:

1. If there is to be N_A molecules of CO₂, there must be:
• N_A carbon atoms and
• (N_A × 2 = 2N_A) oxygen atoms
2. What is the mass of N_A carbon atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A carbon atoms is GAM of carbon which is equal to 12 grams
3. What is the mass of N_A oxygen atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A oxygen atoms is GAM of oxygen which is equal to 16 grams
• So mass of 2N_A oxygen atoms = 2 × 16 = 32 grams 
4. It seems that 12 grams of carbon and 32 grams of oxygen will give us N_A carbon dioxide molecules. Let us check: 
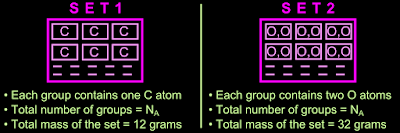
5. Let us consider (12+32) = 44 grams of water. Let this '44 grams' consist of 12 grams of carbon  and 32 grams of oxygen  
6. We can group it in the following way:
• The N_A carbon atoms (obtained from 12 grams of carbon) should be split into N_A groups, so that, each group has 1 carbon atom
• The 2N_A oxygen atoms (obtained from 32 grams of oxygen) should also be split into N_A groups, so that, each group has 2 oxygen atoms
7. Thus the 12 grams of carbon is now split into N_A groups. Let this be Set 1
• The 32 grams of oxygen is also now split into N_A groups. Let this be Set 2
The two sets are shown in fig.10.4 below:

Fig.10.4

8. Both the sets have the same number (N_A) of groups
• So each group from Set 1 will get a partner from Set 2
9. When a group from Set 1 (consisting of one carbon atom) enter into partnership with a group from Set 2 (consisting of two oxygen atoms), we get a molecule (CO₂) of carbon dioxide
10. Since there are N_A groups in each set, we will get N_A carbon dioxide molecules
11. Thus we can conclude: 44 grams of carbon dioxide will give N_A carbon dioxide molecules

One more example: Consider a molecule of glucose (C₆H₁₂O₆). How many grams of glucose should we take so that, there will be N_A molecules of C₆H₁₂O₆?
Solution:
1. If there is to be N_A molecules of C₆H₁₂O₆, there must be:
• (N_A × 6 = 6N_A) carbon atoms
• (N_A × 12 = 12N_A) hydrogen atoms
• (N_A × 6 = 6N_A) oxygen atoms
2. What is the mass of N_A carbon atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A carbon atoms is GAM of carbon which is equal to 12 grams
• So mass of 6N_A carbon atoms = 6 × 12 = 72 grams 
3. What is the mass of N_A hydrogen atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A hydrogen atoms is GAM of oxygen which is equal to 1 gram
• So mass of 12N_A oxygen atoms = 12 × 1 = 12 grams 
4. What is the mass of N_A oxygen atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A oxygen atoms is GAM of oxygen which is equal to 16 grams
• So mass of 6N_A oxygen atoms = 6 × 16 = 96 grams 
5. It seems that 72 grams of carbon, 12 grams of hydrogen and 96 grams of oxygen will give us N_A carbon glucose molecules. Let us check: 
6. Let us consider (72+12+96) = 180 grams of glucose. Let this '180 grams' consist of 72 grams of carbon, 12 grams of hydrogen  and 96 grams of oxygen  
7. We can group it in the following way:
• The 6N_A carbon atoms (obtained from 72 grams of carbon) should be split into N_A groups, so that, each group has 6 carbon atoms
• The 12N_A hydrogen atoms (obtained from 12 grams of hydrogen) should also be split into N_A groups, so that, each group has 12 hydrogen atoms
• The 6N_A oxygen atoms (obtained from 96 grams of oxygen) should also be split into N_A groups, so that, each group has 6 oxygen atoms
8. Thus the 72 grams of carbon is now split into N_A groups. Let this be Set 1
• The 12 grams of hydrogen is also now split into N_A groups. Let this be Set 2
• The 96 grams of oxygen is also now split into N_A groups. Let this be Set 3
The three sets are shown in fig.10.5 below:

Fig.10.5

9. All the three sets have the same number (N_A) of groups
• So each group from Set 1 will get a partner from Set 2 and set 3
10. When a group from Set 1 (consisting of six carbon atoms) enter into partnership with a group from Set 2 (consisting of twelve hydrogen atoms) and a group from Set 3 (consisting of six oxygen atoms), we get a molecule (C₆H₁₂O₆) of glucose
11. Since there are N_A groups in each set, we will get N_A glucose molecules
12. Thus we can conclude: 180 grams of glucose will give N_A  glucose molecules

Let us write a summary of the above discussion on molecules:
■ Molecules of elements:
• To get N_A hydrogen molecules, we must take 2 grams of hydrogen atoms 
• To get N_A oxygen molecules, we must take 32 grams of oxygen atoms 
• To get N_A ozone molecules, we must take 48 grams of oxygen atoms
• To get N_A sulphur molecules, we must take 256 grams of sulphur atoms 
• To get N_A helium molecules, we must take 4 grams of helium atoms
■ Molecules of compounds
• To get N_A water molecules, we must take 18 grams of water
• To get N_A carbon dioxide molecules, we must take 44 grams of carbon dioxide
• To get N_A glucose molecules, we must take 180 grams of glucose

---

Is there an easier method to get the above masses? Let us try:

■ Consider a molecule of hydrogen. 
1. The molecule is H₂. It has two hydrogen atoms. 
2. So total mass of a molecule of hydrogen will be twice the mass of a hydrogen atom
3. We know that, the mass of a hydrogen atom is 1 u
4. So mass of a hydrogen molecule = (2 × 1 u) = 2 u
5. Above we found that, to get N_A hydrogen molecules, we must take 2 grams of hydrogen atoms   
• In (4) we have 2 u. 
• In (5) we have 2 grams
• The numeric parts are the same 

■ Consider a molecule of oxygen. 
1. The molecule is O₂. It has two oxygen atoms. 
2. So total mass of a molecule of oxygen will be twice the mass of a oxygen atom
3. We know that, the mass of a oxygen atom is 16 u
4. So mass of a oxygen molecule = (2 × 16 u) = 32 u
5. Above we found that, to get N_A oxygen molecules, we must take 32 grams of oxygen atoms   
• In (4) we have 32 u. 
• In (5) we have 32 grams
• The numeric parts are the same

■ Consider a molecule of ozone. 
1. The molecule is O₃. It has three oxygen atoms. 
2. So total mass of a molecule of ozone will be thrice the mass of a oxygen atom
3. We know that, the mass of a oxygen atom is 16 u
4. So mass of a ozone molecule = (3 × 16 u) = 48 u
5. Above we found that, to get N_A ozone molecules, we must take 48 grams of oxygen atoms   
• In (4) we have 48 u. 
• In (5) we have 48 grams
• The numeric parts are the same

■ Consider a molecule of sulphur. 
1. The molecule is S₈. It has eight sulphur atoms. 
2. So total mass of a molecule of sulphur will be eight times the mass of a sulphur atom
3. We know that, the mass of a sulphur atom is 32 u
4. So mass of a sulphur molecule = (8 × 32 u) = 256 u
5. Above we found that, to get N_A sulphur molecules, we must take 256 grams of sulphur atoms   
• In (4) we have 256 u. 
• In (5) we have 256 grams
• The numeric parts are the same

■ Consider a molecule of helium. 
1. The molecule is H. It has only one helium atom. 
2. So total mass of a molecule of helium will be same as the mass of a helium atom
3. We know that, the mass of a helium atom is 4 u
4. So mass of a helium molecule = (1 × 4 u) = 4 u
5. Above we found that, to get N_A helium molecules, we must take 4 grams of helium atoms   
• In (4) we have 4 u. 
• In (5) we have 4 grams
• The numeric parts are the same

■ Consider a molecule of water. 
1. The molecule is H₂O. It has two hydrogen atoms and one oxygen atom. 
2. So total mass of a molecule of water will be the sum of:
• twice the mass of a hydrogen atom
• mass of  an oxygen atom
3. We know that, the mass of a hydrogen atom is 1 u and that of oxygen atom is 16 u
4. So mass of a water molecule = (2 × 1 u) + (1 × 16 u)   = 2 u + 16 u = 18 u
5. Above we found that, to get N_A water molecules, we must take 18 grams of water 
• In (4) we have 18 u. 
• In (5) we have 18 grams
• The numeric parts are the same

■ Consider a molecule of carbon dioxide. 
1. The molecule is CO₂. It has one carbon atom and two oxygen atoms. 
2. So total mass of a molecule of carbon dioxide will be the sum of:
• mass of a carbon atom
• twice the mass of an oxygen atom
3. We know that, the mass of a carbon atom is 12 u and that of oxygen atom is 16 u
4. So mass of a carbon dioxide molecule = (1 × 12 u) + (2 × 16 u)   = 12 u + 32 u = 44 u
5. Above we found that, to get N_A carbon dioxide molecules, we must take 44 grams of carbon dioxide
• In (4) we have 44 u. 
• In (5) we have 44 grams
• The numeric parts are the same

■ Consider a molecule of glucose. 
1. The molecule is C₆H₁₂O₆. It has six carbon atoms, twelve hydrogen atoms and six oxygen atoms. 
2. So total mass of a molecule of glucose will be the sum of:
• six times the mass of a carbon atom
• twelve times the mass of a hydrogen atom
• six times the mass of an oxygen atom
3. We know that, the mass of a carbon atom is 12 u, mass of a hydrogen atom is 1 u and that of an oxygen atom is 16 u
4. So mass of a glucose molecule = (6 × 12 u) + (12 × 1 u) + (6 × 16 u) = 72 u + 12 u + 96 u = 180 u
5. Above we found that, to get N_A glucose molecules, we must take 180 grams of glucose
• In (4) we have 180 u. 
• In (5) we have 180 grams
• The numeric parts are the same

---

So we can write:

• Each molecule (it may be 'a molecule of an element' or 'a molecule of a compound') will have a unique value for the 'mass in grams' 

• If we take that much mass of that element/compound, there will be N_A number of molecules

• This unique mass is called 'Gram Molecular Mass' (GMM) of that molecule
Some examples:
• GMM of element oxygen is 16 grams
    ♦ In 16 grams of oxygen, there will be N_A molecules of oxygen
• GMM of element helium is 4 grams
    ♦ In 4 grams of helium, there will be N_A molecules of helium
• GMM of compound glucose is 180 grams
    ♦ In 180 grams of glucose, there will be N_A molecules of glucose

---

The GMM of any molecule can be written using the following steps

Step 1: Calculate the total mass of one molecule. It's unit will be in 'u'
Step 2: Write the numeric part
Step 3: Write 'grams' on the right side
This will give the GMM of that molecule

---

Some examples:

1. Find the GMM of ammonia (NH₃)
Solution:
Step 1: Total mass of one molecule:
Mass of one nitrogen atom = 14 u
Mass of one hydrogen atom = 1 u
So total mass = (1 × 14 u) + (3 × 1 u) = 14 u + 3 u = 17 u
Step 2: Write the numeric part: 17
Step 3: Write 'grams' on the right side. We get: 17 grams
So GMM of ammonia is 17 grams

1. Find the GMM of HCl
Solution:
Step 1: Total mass of one molecule:
Mass of one hydrogen atom = 1 u
Mass of one chlorine atom = 35.5 u
So total mass = (1 × 1 u) + (1 × 35.5 u) = 1 u + 35.5 u = 36.5 u
Step 2: Write the numeric part: 36.5
Step 3: Write 'grams' on the right side. We get: 36.5 grams
So GMM of ammonia is 36.5 grams

---

Once we understand the basics, there will not be any need to write the steps. Just write the total mass of one molecule, and write 'grams' instead of 'u'

We will now see some solved examples

Solved example 10.1
How many water molecules are present in 90 grams of water?
Solution:
1. GMM of water (H₂O) = (2 × 1) + (1 × 16) = 2 + 16 = 18 grams
2. No. of GMMs in 90 grams of water = ⁹⁰⁄₁₈  = 5
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 5 GMMs = 5N_A = 5 × 6.022×10²³

---

Let us do the above problem by another method, which uses some very basic information:

1. We have:
No. of molecules ×  Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 90 grams
3. Mass (in u) of one molecule of water = (2 × 1) + (1 × 16) = 2 + 16 = 18 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 18 u = 18 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 5 × 6.022×10²³ that we got earlier.  
In these types of problems, it is worthy to always remember that, the reciprocal of 'u in grams' gives the Avogadro number N_A. That is:      

We can check it using a calculator

---

Solved example 10.2

Samples of some compounds are given:
(i) 85 grams of ammonia (NH₃) 
(ii) 90 grams of glucose (C₆H₁₂O₆)
(iii) 88 grams of carbon dioxide (CO₂)
(iv) 50 grams of hydrogen (H₂)  
• Find the number of molecules in each sample. (Hint: GAMs are: H = 1g, C = 12 g, N = 14 g, O = 16 g)
Solution (i):
1. GMM of ammonia (NH₃) = (1 × 14) + (1 × 3) = 14 + 3 = 17 grams
Note: For this step we require the atomic masses (in u) of nitrogen and hydrogen. But they are given to us in the form of GAM. We know that, GAM is numerically same as u. 
2. No. of GMMs in 85 grams of water = ⁸⁵⁄₁₇  = 5
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 5 GMMs = 5N_A = 5 × 6.022×10²³

---

Let us do the problem by another method, which uses some very basic information:

1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 85 grams
3. Mass (in u) of one molecule of water = (1 × 14) + (1 × 3) = 14 + 3 = 17 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 18 u = 18 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 5 × 6.022×10²³ that we got earlier.

Solution (ii):
1. GMM of glucose (C₆H₁₂O₆) = (6 × 12) + (1 × 12) + (6 × 16) = 72 + 12 + 96 = 180 grams
2. No. of GMMs in 90 grams of water = ⁹⁰⁄₁₈₀  = 0.5
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 0.5 GMMs = 0.5N_A = 0.5 × 6.022×10²³

---

Let us do the above problem by the other method:

1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 90 grams
3. Mass (in u) of one molecule of glucose = (6 × 12) + (1 × 12) + (6 × 16) = 72 + 12 + 96 = 180 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 180 u = 180 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 0.5 × 6.022×10²³ that we got earlier.  

Solution (iii):
1. GMM of carbon dioxide (CO₂) = (1 × 12) + (16 × 2) = 12 + 32 = 44 grams
2. No. of GMMs in 88 grams of water = ⁸⁸⁄₄₄  = 2
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 2 GMMs = 2N_A = 2 × 6.022×10²³

---

Let us do the above problem by the other method:

1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 88 grams
3. Mass (in u) of one molecule of carbon dioxide = (1 × 12) + (16 × 2) = 12 + 32 = 44 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 44 u = 44 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 2 × 6.022×10²³ that we got earlier.

Solution (iv):
1. GMM of hydrogen (H₂) = (2 × 1) = 2 grams
2. No. of GMMs in 50 grams of water = ⁵⁰⁄₂  = 25
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 25 GMMs = 25N_A = 25 × 6.022×10²³

---

Let us do the above problem by the other method:

1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 50 grams
3. Mass (in u) of one molecule of glucose = (2 × 1) = 2 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 2 u = 2 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 2 × 6.022×10²³ that we got earlier.

---

Based on the above discussion, we can now take up 'mole'. We will see it in the next section. 

PREVIOUS      CONTENTS       NEXT

                        Copyright©2017 High school Chemistry lessons. blogspot.in - All Rights Reserved

Chapter 9.6 - Properties of d-block and f-block elements

In the previous section, we saw the properties of s-block and p-block elements.  In this section we will see the properties of d-block elements.

Properties of d-block elements 

■ Position: The d-block consists of the groups from 3 to 12 of the periodic table
■ Common names:
The elements of the groups from 3 to 12 are known as transition elements
■ Oxidation state
• Let us find the oxidation state of Fe in FeCl₂. 
We have seen the method of calculation here. From the table we have: oxidation state of Cl = -1
Let the oxidation state of Fe be 'x'. Then we get: x + 2 × -1 = 0 ⇒ x -2 = 0 ⇒ x = +2   
So the oxidation state of Fe in FeCl₂ is +2
• Let us find the oxidation state of Fe in FeCl₃. 
From the table we have: oxidation state of Cl = -1
Let the oxidation state of Fe be 'x'. Then we get: x + 3 × -1 = 0 ⇒ x -3 = 0 ⇒ x = +3   
So the oxidation state of Fe in FeCl₃ is +3
• So we see that Fe shows variable oxidation states. Let us analyse and find the reason for this:
1. The S.E.C of  Fe is: 1s²2s²2p⁶3s²3p⁶4s²3d⁶ . 
Fe loses two electrons and becomes Fe²⁺. The two electrons are lost from the s subshell in the outermost main shell. That is., the 4s subshell. 
So the S.E.C of  Fe²⁺ is: 1s²2s²2p⁶3s²3p⁶3d⁶ .
2. The S.E.C of  Fe is: 1s²2s²2p⁶3s²3p⁶4s²3d⁶ . 
Fe loses three electrons and becomes Fe³⁺. 
First, two electrons are lost from the s subshell in the outermost main shell. That is., the 4s subshell. 
Then one electron is lost from the d subshell in the penultimate main shell. That is., the 3d subshell. 
So the S.E.C of  Fe³⁺ is: 1s²2s²2p⁶3s²3p⁶3d⁵.
• When we consider the main shells alone, this phenomenon cannot be explained. 
• But the explanation becomes clear when we consider subshells also:
• The difference in energy between 3d subshell and 4s subshell is very small. So, under suitable conditions, the electron in 3d subshell also take part in chemical reactions. 
• This accounts for the variable oxidation states shown by transition elements  

Another example:
• Let us find the oxidation state of Mn in MnCl₂. 
We have seen the method of calculation here. From the table we have: oxidation state of Cl = -1
Let the oxidation state of Mn be 'x'. Then we get: x + 2 × -1 = 0 ⇒ x -2 = 0 ⇒ x = +2   
So the oxidation state of Mn in MnCl₂ is +2
• Let us find the oxidation state of Mn in MnO₂. 
From the table we have: oxidation state of O = -2
Let the oxidation state of Mn be 'x'. Then we get: x + 2 × -2 = 0 ⇒ x -4 = 0 ⇒ x = +4   
So the oxidation state of Mn in MnO₂ is +4
• Let us find the oxidation state of Mn in Mn₂O₃. 
From the table we have: oxidation state of O = -2
Let the oxidation state of Mn be 'x'. Then we get: 2 × x + 3 × -2 = 0 ⇒ 2x -6 = 0 ⇒ x = +3   
So the oxidation state of Mn in Mn₂O₃ is +3
• Let us find the oxidation state of Mn in Mn₂O₇. 
From the table we have: oxidation state of O = -2
Let the oxidation state of Mn be 'x'. Then we get: 2 × x + 7 × -2 = 0 ⇒ 2x -14 = 0 ⇒ x = +7   
So the oxidation state of Mn in Mn₂O₇ is +7

---

1. The S.E.C of Mn is: 1s²2s²2p⁶3s²3p⁶4s²3d⁵.

Mn loses two electrons and becomes Mn²⁺. The two electrons are lost from the s subshell in the outermost main shell. That is., the 4s subshell. 
So the S.E.C of  Mn²⁺ is: 1s²2s²2p⁶3s²3p⁶3d⁵ . 
2. The S.E.C of  Mn is: 1s²2s²2p⁶3s²3p⁶4s²3d⁵ . 
Mn loses four electrons and becomes Mn⁴⁺. 
First, two electrons are lost from the s subshell in the outermost main shell. That is., the 4s subshell. 
Then two electrons are lost from the d subshell in the penultimate main shell. That is., the 3d subshell. 
So the S.E.C of  Mn⁴⁺ is: 1s²2s²2p⁶3s²3p⁶3d³.
3. The S.E.C of  Mn is: 1s²2s²2p⁶3s²3p⁶4s²3d⁶ . 
Mn loses three electrons and becomes Mn³⁺. 
First, two three electrons are lost from the s subshell in the outermost main shell. That is., the 4s subshell. 
Then one electron is lost from the d subshell in the penultimate main shell. That is., the 3d subshell. 
So the S.E.C of  Mn³⁺ is: 1s²2s²2p⁶3s²3p⁶3d⁴.
4. The S.E.C of  Mn is: 1s²2s²2p⁶3s²3p⁶4s²3d⁵ . 
Mn loses seven electrons and becomes Mn⁷⁺. 
First, two electrons are lost from the s subshell in the outermost main shell. That is., the 4s subshell. 
Then five electrons are lost from the d subshell in the penultimate main shell. That is., the 3d subshell. 
So the S.E.C of  Mn⁴⁺ is: 1s²2s²2p⁶3s²3p⁶.
• We see that electrons in the d subshell in the penultimate main shell also takes partin the reactions. 
• This is because, the difference in energy level between the following two is very low:
    ♦ s subshell in the outermost main shell
    ♦ d subshell in the penultimate main shell
• So transition elements in general show variable oxidation states
■ Metallic property
The transition elements are metals
■ Coloured compounds
Most of the compounds formed by transition elements are coloured. Some examples are given below:
• Copper sulphate is a compound of copper, which is a transition element. This compound is blue in colour  
• Cobalt nitrate is a compound of cobalt, which is a transition element. This compound is light pink in colour
• Potassium permanganate is a compound of manganese, which is a transition element. This compound is violet in colour    
• Ferrous sulphate is a compound of iron, which is a transition element. This compound is light green in colour  
• Ammonium dichromate is a compound of chromium, which is a transition element. This compound is orange in colour  
• Compounds of transition elements are used to give colour to glass, prepare some dyes etc.,
■ Uses of transition elements
• Copper is used for making electric cables
• Nickel is used for making coins
• Titanium is used aircraft parts

Properties of f-block elements 

■ Position: The f-block elements are those elements which are placed in two rows at the bottom of the periodic table. We have seen the reason for placing them separately in an earlier chapter. Details here.
The elements of the first row are called Lanthanoids and those in the second row are called Actinoids. They belong to the sixth and seventh periods respectively.
■ S.E.C:
• We know that, the last electron of each element in the f-block will be filled in the f subshell. 
Let us examine the S.E.C of two elements:
• First we will consider ₅₈Ce (Cerium). It is a Lanthanoid 
It has the S.E.C: [Xe]4f¹5d¹6s². 
From the S.E.C it is clear that, cerium falls in the 6^th period.
The last main shell is 6. But the last electron falls in the f subshell of the main shell 4. That is., 4f    
• Next we will consider ₉₀Th (Thorium). It is an Actinoid 
It has the S.E.C: [Rn]5f³6d¹7s². 
From the S.E.C it is clear that, thorium falls in the 7^th period.
The last main shell is 7. But the last electron falls in the f subshell of the main shell 5. That is., 5f

---

So we can write:

• f-block elements Lanthanoids belong to the 6^th period. Their last electrons are filled in the 4f subshell 
• f-block elements Actinoids belong to the 7^th period. Their last electrons are filled in the 5f subshell 

---

■ Characteristics and uses of f-block elements

• Most of the f-block elements show variable oxidation states like the d-block elements

• Most of the actinoids are radioactive and are artificial elements

• Uranium, thorium, plutonium etc., are used as fuels in nuclear reactors

• Many of them are used as catalysts in the petroleum industry

---

Now we will see some solved examples

Solved example 9.7

The element X in group 17 has 3 shells. If so,

(i) Write the S.E.C of the element

(ii) Write the period number

(iii)What will be the chemical formula of the compound formed if the element X reacts with element Y of the third period which contains one electron in the p subshell?

Solution:
Part (i):
1. We have two clues:
• The element belongs to group 17
    ♦ From this it is clear that it belongs to the p-block
• It has 3 shells
    ♦ From this it is clear that it belongs to the 3^rd period
2. For any element in the p-block, the group number is obtained as follows:
• Number of electrons in the p subshell of the last main shell + 12
3. So we can write: 17 =  Number of electrons in the p subshell of the 3^rd main shell + 12
• Thus we get: Number of electrons in the p subshell of the 3^rd main shell = 5
4. For any element in the p-block, the last electron is filled in the p subshell of the last main shell
So we can write:
• The last term of the S.E.C is 3p⁵.
5. If the last term is 3p⁵, the preceding terms will be:
1s²2s²2p⁶3s².
• So the S.E.C is: 1s²2s²2p⁶3s²3p⁵. 
Part (ii):
The period number is 3
Part (iii):
1. First we will write the S.E.C of element Y
We have two clues:
• The element belongs to the third period
    ♦ From this it is clear that the suffix of the last term of the S.E.C is 3
• It has one electron in the p subshell
    ♦ The p subshell can hold 6 electrons. So, if there is only one electron, it will be the last electron
    ♦ So the last term is 3p¹
If the last term is 3p¹, the preceding terms will be:
1s²2s²2p⁶3s²
• So the S.E.C is: 1s²2s²2p⁶3s²3p¹. 
2. The last main shell has 3 electrons. So the valency of element Y is 3
From the S.E.C of element X, it's valency is 8 -7 = 1
3. We have seen how to write the chemical formula from valency. Details here.
4. We have to find the element with lower electronegativity between X and Y 
From the S.E.C of Y, the group number of Y is 13
(Number of electrons in the p subshell of the 3^rd main shell + 12 = 1 + 12 = 13)
So Y is in the group 13 and period 3. X is in group 17 and same period
Y is on the left of X in the same period
Thus Y is less electronegative than X
So Y is to be written first
5. So the required chemical formula is YX₃

Solved example 9.8

The element Cu with atomic number 29 undergoes chemical reaction to form an ion with oxidation state +2

(i) Write down the S.E.C of this ion

(ii) Can Cu show variable valency? Why?

(iii) Write down the chemical formula of one compound formed when Cu reacts with ₁₇Cl. 
Solution:
Part (i):
1. The S.E.C of Cu (copper) is 1s²2s²2p⁶3s²3p⁶4s¹3d¹⁰  OR [Ar]4s¹3d¹⁰.
2. There is only a small energy difference between 4s and 3d subshells. So if conditions are favourable,  electrons in the 3d subshell may also take part in chemical reactions
3. When two electrons are lost to form +2 oxidation state, it is clear that, one electron from the 3d is also lost in addition to the last electon in 4s
4. So the S.E.C of the ion is: 1s²2s²2p⁶3s²3p⁶3d⁹.
Part (ii)
Cu can show variable valency because, if conditions are favourable,  electrons in the 3d subshell may also take part in chemical reactions  
Part (iii):
1. The S.E.C of Chlorine is: 1s²2s²2p⁶3s²3p⁵.
It requires 1 more electron to complete octect. So it's valency is 1
2. Cu is ready to give two electrons. One from the 4s subshell and the other from the 3d subshell. So it's valency is 2
3. We have seen how to write the chemical formula from valency. Details here. 
4. Thus the chemical formula of the compound is CuCl₂. 
Note that Cu, which has a lower electronegativity is written first.

---

We have completed our present discussion about Subshell electronic configuration and properties of various blocks. In the next section, we will see Mol concept. 

PREVIOUS      CONTENTS       NEXT

                        Copyright©2017 High school Chemistry lessons. blogspot.in - All Rights Reserved