Chapter 10.4 - Number of Moles of Atoms and Molecules

In the previous section, we saw GMM. In this section we will see the details about 'mole':

We have seen that,
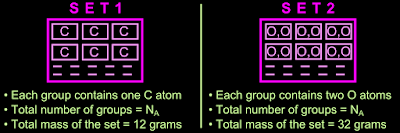
• 1 GAM of any element will contain N_A atoms
    ♦ That is., 6.022×10²³ atoms
• 1 GMM of any element/compound will contain N_A molecules
    ♦ That is., 6.022×10²³ molecules
■ This 6.022×10²³ is a very important number in chemistry. So it is given a special name: mole.
Let us see a comparison:
• Consider a group of apples. If there are 12 apples in that group, we say: A dozen apples
• Consider a group of atoms. If there are 6.022×10²³ atoms in that group, we say: A mole atoms
• Consider a group of molecules. If there are 6.022×10²³ molecules in that group, we say: A mole molecules
• Consider a group of ions. If there are 6.022×10²³ ions in that group, we say: A mole ions
■ While using mole, it is important to specify the name of the particle. That is., whether it is atom, molecule or ion.

---

Based on the above discussion, a relation can be established between two sides. One side consists of the mole. The other side consists of Avogadro number (N_A), GAM and GMM. The fig.10.6 below illustrates the relation:

Fig.10.6

■ The definition for mole can be written as follows:
The amount of any substance containing 6.022×10²³ particles is called one mole (1 mole or 1 mol)

---

The concept will become more clear when we see some solved examples 

Solved example 10.3
A sample of water contains 10,000 water molecules. How many moles of molecules are present in it?
Solution:
1. One mole of molecules will contain 6.022×10²³ molecules.
2. So no. of moles in 10000 molecules = ¹⁰⁰⁰⁰⁄_{(6.022 × 10²³)} 

Solved example 10.4
Find the number of moles in the following:
(i) 1,00,000 CO₂ molecules
(ii) 1,00,000 H₂ molecules
(iii) 6.022×10²³ glucose molecules   
Solution (i):
1. One mole of molecules will contain 6.022×10²³ molecules.
2. So no. of moles in 1,00,00 molecules = ¹⁰⁰⁰⁰⁰⁄_{(6.022 × 10²³)} 
That is., 1,00,000 CO₂ molecules will contain [¹⁰⁰⁰⁰⁰⁄_{(6.022 × 10²³)}] moles
Solution (ii):
1. One mole of molecules will contain 6.022×10²³ molecules.
2. So no. of moles in 1,00,00 molecules = ¹⁰⁰⁰⁰⁰⁄_{(6.022 × 10²³)} .
That is., 1,00,000 H₂ molecules will contain [¹⁰⁰⁰⁰⁰⁄_{(6.022 × 10²³)}] moles
Solution (iii):
1. One mole of molecules will contain 6.022×10²³ molecules.
2. So no. of moles in 6.022×10²³ molecules = ^{(6.022 × 1023)}⁄_{(6.022 × 10²³)} = 1
That is., 6.022×10²³ glucose molecules will contain 1 mole

Solved example 10.5
Find the number of moles of atoms in 160 grams of oxygen
Solution:
1. One mole of atoms will contain 6.022×10²³ atoms.
• So no. of moles of atoms = ^{(Total no. of atoms)}⁄_{(6.022 × 10²³)} .
2. But we are not given 'Total no. of atoms'. We have to calculate it from the given 'total mass'
• Given total mass = 160 g
3. 1 GAM of oxygen will contain 6.022×10²³ atoms of oxygen
• 1 GAM of oxygen = 16 g
• No. of GAMs in 160 g = ¹⁶⁰⁄₁₆ = 10
4. So no. of atoms in 160 g = 10 × 6.022×10²³
5. Substituting this in (1) we get:
No. of moles of atoms = ^{(Total no. of atoms)}⁄_{(6.022 × 10²³)} = ^{(10×6.022×1023)}⁄_{(6.022×10²³)} = 10
• We can write the above result in the form of an equation:
Eq.10.1:
No. of moles of atoms/molecules = ^{(Total no. of atoms/molecules)}⁄_NA

■ Another method using basic information:
1. We have:
No. of atoms × Mass (in grams) of one atom = Given total Mass (in grams)
⇒ No. of atoms = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one atom}.  
2. Given total mass = 160 grams
3. Mass (in u) of one atom of oxygen = 16 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 16 u = 16 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:
No. of atoms = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one atom} 
= ¹⁶⁰⁄_{(16×1.6605×10^-24)} = ¹⁰⁄_{(1.6605×10^-24)}
6. No. of moles of atoms = ^{No. of atoms}⁄_{(6.022×10²³)} 
= [¹⁰⁄_{(1.6605×10^-24)}] ÷ 6.022×10²³ = [¹⁰⁄_{(1.6605×10^-24)}] × [¹⁄_{(6.022 × 10²³)}] 
7. But ¹⁄_{(6.022 × 10²³)} = 1.6605×10^-24. So numerator and denominator will cancel each other.  We get 10 as the answer

Solved example 10.6
Find the number of moles of molecules in 160 grams of oxygen
Solution:
1. One mole of molecules will contain 6.022×10²³ molecules.
• So no. of moles = ^{(Total no. of molecules)}⁄_{(6.022 × 10²³)} .
2. But we are not given 'Total no. of molecules'. We have to calculate it from the given 'total mass'
• Given total mass = 160 g
3. 1 GMM of oxygen will contain 6.022×10²³ molecules of oxygen
• 1 GMM of oxygen = 32 g
• No. of GMMs in 160 g = ¹⁶⁰⁄₃₂ = 5
4. So no. of molecules in 160 g = 5 × 6.022×10²³
5. Substituting this in (1) we get:
No. of moles = ^{(Total no. of molecules)}⁄_{(6.022 × 10²³)} = ^{(5×6.022×1023)}⁄_{(6.022×10²³)} = 5

■ Another method using basic information:
1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule} .  
2. Given total mass = 160 grams
3. Mass (in u) of one molecule of oxygen = 32 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 32 u = 32 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:
No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one atom} 
= ¹⁶⁰⁄_{(32×1.6605×10^-24)} = ⁵⁄_{(1.6605×10^-24)}
6. No. of moles of molecules = ^{No. of molecules}⁄_{(6.022×10²³)} 
= [⁵⁄_{(1.6605×10^-24)}] ÷ 6.022×10²³ = [⁵⁄_{(1.6605×10^-24)}] × [¹⁄_{(6.022 × 10²³)}] 

7. But ¹⁄_{(6.022 × 10²³)} = 1.6605×10^-24. So numerator and denominator will cancel each other.  We get 5 as the answer

Solved example 10.7
Find the number of moles of molecules in 220 grams of CO₂
Solution:
1. One mole of molecules will contain 6.022×10²³ molecules.
• So no. of moles = ^{(Total no. of molecules)}⁄_{(6.022 × 10²³)}
2. But we are not given 'Total no. of molecules'. We have to calculate it from the given 'total mass'
• Given total mass = 220 g
3. 1 GMM of CO₂ will contain 6.022×10²³ molecules of CO₂
• 1 GMM of CO₂ = (1×12) + (2×16) = 12 + 32 = 44 g
• No. of GMMs in 220 g = ²²⁰⁄₄₄ = 5
4. So no. of molecules in 220 g = 5 × 6.022×10²³
5. Substituting this in (1) we get:
No. of moles = ^{(Total no. of molecules)}⁄_{(6.022 × 10²³)} = ^{(5×6.022×1023)}⁄_{(6.022×10²³)} = 5

■ Another method using basic information:
1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule} .  
2. Given total mass = 220 grams
3. Mass (in u) of one molecule of CO₂ = (1×12) + (2×16) = 12 + 32 = 44 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 44 u = 44 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:
No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one atom} 
= ²²⁰⁄_{(44×1.6605×10^-24)} = ⁵⁄_{(1.6605×10^-24)}
6. No. of moles of molecules = ^{No. of molecules}⁄_{(6.022×10²³)} 
= [⁵⁄_{(1.6605×10^-24)}] ÷ 6.022×10²³ = [⁵⁄_{(1.6605×10^-24)}] × [¹⁄_{(6.022 × 10²³)}] 

7. But ¹⁄_{(6.022 × 10²³)} = 1.6605×10^-24. So numerator and denominator will cancel each other.  We get 5 as the answer

Solved example 10.8
Find 
(i) The number of moles of atoms in 700 grams of nitrogen
(ii) The number of moles of molecules in 700 grams of nitrogen
(iii) Number of moles of sugar molecules in 1 kg of sugar (C₁₂H₂₂O₁₁) and the number of moles of carbon atoms present in that 1 kg
(iv) Number of moles in 3.011×10²³ carbon atoms
Solution (i):
1. One mole of atoms will contain 6.022×10²³ atoms.
• So no. of moles = ^{(Total no. of atoms)}⁄_{(6.022 × 10²³)} .
2. But we are not given 'Total no. of atoms'. We have to calculate it from the given 'total mass'
• Given total mass = 700 g
3. 1 GAM of nitrogen will contain 6.022×10²³ atoms of nitrogen
• 1 GAM of nitrogen = 14 g
• No. of GAMs in 700 g = ⁷⁰⁰⁄₁₄ = 50
4. So no. of atoms in 700 g = 50 × 6.022×10²³
5. Substituting this in (1) we get:
No. of moles = ^{(Total no. of atoms)}⁄_{(6.022 × 10²³)} = ^{(50×6.022×1023)}⁄_{(6.022×10²³)} = 50

Solution (ii):
1. One mole of molecules will contain 6.022×10²³ molecules.
• So no. of moles = ^{(Total no. of molecules)}⁄_{(6.022 × 10²³)}
2. But we are not given 'Total no. of molecules'. We have to calculate it from the given 'total mass'
• Given total mass = 700 g
3. 1 GMM of nitrogen will contain 6.022×10²³ molecules of nitrogen
• 1 GMM of nitrogen = 28 g
• No. of GMMs in 700 g = ⁷⁰⁰⁄₂₈ = 25
4. So no. of molecules in 700 g = 25 × 6.022×10²³
5. Substituting this in (1) we get:
No. of moles = ^{(Total no. of molecules)}⁄_{(6.022 × 10²³)} = ^{(25×6.022×1023)}⁄_{(6.022×10²³)} = 25
Solution (iii):

1. One mole of molecules will contain 6.022×10²³ molecules.
• So no. of moles = ^{(Total no. of molecules)}⁄_{(6.022 × 10²³)}
2. But we are not given 'Total no. of molecules'. We have to calculate it from the given 'total mass'
• Given total mass = 1 kg = 1000 g
3. 1 GMM of C₁₂H₂₂O₁₁ will contain 6.022×10²³ molecules of C₁₂H₂₂O₁₁
• 1 GMM of C₁₂H₂₂O₁₁ = (12×12) + (22×1) + (11×16) = 144 + 22 + 176 = 342 g
• No. of GMMs in 1000 g = ¹⁰⁰⁰⁄₃₄₂ = 2.92
4. So no. of molecules in 1000 g = 2.92 × 6.022×10²³
5. Substituting this in (1) we get:
No. of moles = ^{(Total no. of molecules)}⁄_{(6.022 × 10²³)} = ^{(2.92×6.022×1023)}⁄_{(6.022×10²³)} = 2.92
6. From (4) we get the total number of sugar molecules as 2.92 × 6.022×10²³.

7. Each of these molecules will contain 12 carbon atoms. 
So total number of carbon atoms in the 1000 grams of sugar = 12 × 2.92 × 6.022×10²³.
8. So no. of moles of carbon atoms = ^{(Total no. of atoms)}⁄_{(6.022 × 10²³)} 
= ^{(12×2.92×6.022×1023)}⁄_{(6.022×10²³)} = 12×2.92 = 35.04 moles
Solution (iv):
1. One mole of atoms will contain 6.022×10²³ atoms.
• So no. of moles = ^{(Total no. of atoms)}⁄_{(6.022 × 10²³)}
2. We are given 'Total no. of atoms'. It is 3.011×10²³.
3. So no. of moles of carbon atoms = ^{(Total no. of atoms)}⁄_{(6.022 × 10²³)} 
= ^{(3.011×1023)}⁄_{(6.022×10²³)} = 0.5 moles

---

So we now know how to convert mass into 'number of moles'. We can also convert a given number of atoms/molecules into 'number of moles'. In the next section we will see the reverse. That is., conversion of 'number of moles' into mass. 

PREVIOUS      CONTENTS       NEXT

                        Copyright©2017 High school Chemistry lessons. blogspot.in - All Rights Reserved

Chapter 10.3 - Gram Molecular Mass

In the previous section, we saw that 18 grams of water will give water molecules. In this section we will see two more examples like that:

■ Consider a molecule of carbon dioxide (CO₂). How many grams of carbon dioxide should we take so that, there will be N_A molecules of CO₂?
Solution:

1. If there is to be N_A molecules of CO₂, there must be:
• N_A carbon atoms and
• (N_A × 2 = 2N_A) oxygen atoms
2. What is the mass of N_A carbon atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A carbon atoms is GAM of carbon which is equal to 12 grams
3. What is the mass of N_A oxygen atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A oxygen atoms is GAM of oxygen which is equal to 16 grams
• So mass of 2N_A oxygen atoms = 2 × 16 = 32 grams 
4. It seems that 12 grams of carbon and 32 grams of oxygen will give us N_A carbon dioxide molecules. Let us check: 
5. Let us consider (12+32) = 44 grams of water. Let this '44 grams' consist of 12 grams of carbon  and 32 grams of oxygen  
6. We can group it in the following way:
• The N_A carbon atoms (obtained from 12 grams of carbon) should be split into N_A groups, so that, each group has 1 carbon atom
• The 2N_A oxygen atoms (obtained from 32 grams of oxygen) should also be split into N_A groups, so that, each group has 2 oxygen atoms
7. Thus the 12 grams of carbon is now split into N_A groups. Let this be Set 1
• The 32 grams of oxygen is also now split into N_A groups. Let this be Set 2
The two sets are shown in fig.10.4 below:

Fig.10.4

8. Both the sets have the same number (N_A) of groups
• So each group from Set 1 will get a partner from Set 2
9. When a group from Set 1 (consisting of one carbon atom) enter into partnership with a group from Set 2 (consisting of two oxygen atoms), we get a molecule (CO₂) of carbon dioxide
10. Since there are N_A groups in each set, we will get N_A carbon dioxide molecules
11. Thus we can conclude: 44 grams of carbon dioxide will give N_A carbon dioxide molecules

One more example: Consider a molecule of glucose (C₆H₁₂O₆). How many grams of glucose should we take so that, there will be N_A molecules of C₆H₁₂O₆?
Solution:
1. If there is to be N_A molecules of C₆H₁₂O₆, there must be:
• (N_A × 6 = 6N_A) carbon atoms
• (N_A × 12 = 12N_A) hydrogen atoms
• (N_A × 6 = 6N_A) oxygen atoms
2. What is the mass of N_A carbon atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A carbon atoms is GAM of carbon which is equal to 12 grams
• So mass of 6N_A carbon atoms = 6 × 12 = 72 grams 
3. What is the mass of N_A hydrogen atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A hydrogen atoms is GAM of oxygen which is equal to 1 gram
• So mass of 12N_A oxygen atoms = 12 × 1 = 12 grams 
4. What is the mass of N_A oxygen atoms?
• Mass of N_A atoms of any element is it's GAM
• So mass of N_A oxygen atoms is GAM of oxygen which is equal to 16 grams
• So mass of 6N_A oxygen atoms = 6 × 16 = 96 grams 
5. It seems that 72 grams of carbon, 12 grams of hydrogen and 96 grams of oxygen will give us N_A carbon glucose molecules. Let us check: 
6. Let us consider (72+12+96) = 180 grams of glucose. Let this '180 grams' consist of 72 grams of carbon, 12 grams of hydrogen  and 96 grams of oxygen  
7. We can group it in the following way:
• The 6N_A carbon atoms (obtained from 72 grams of carbon) should be split into N_A groups, so that, each group has 6 carbon atoms
• The 12N_A hydrogen atoms (obtained from 12 grams of hydrogen) should also be split into N_A groups, so that, each group has 12 hydrogen atoms
• The 6N_A oxygen atoms (obtained from 96 grams of oxygen) should also be split into N_A groups, so that, each group has 6 oxygen atoms
8. Thus the 72 grams of carbon is now split into N_A groups. Let this be Set 1
• The 12 grams of hydrogen is also now split into N_A groups. Let this be Set 2
• The 96 grams of oxygen is also now split into N_A groups. Let this be Set 3
The three sets are shown in fig.10.5 below:

Fig.10.5

9. All the three sets have the same number (N_A) of groups
• So each group from Set 1 will get a partner from Set 2 and set 3
10. When a group from Set 1 (consisting of six carbon atoms) enter into partnership with a group from Set 2 (consisting of twelve hydrogen atoms) and a group from Set 3 (consisting of six oxygen atoms), we get a molecule (C₆H₁₂O₆) of glucose
11. Since there are N_A groups in each set, we will get N_A glucose molecules
12. Thus we can conclude: 180 grams of glucose will give N_A  glucose molecules

Let us write a summary of the above discussion on molecules:
■ Molecules of elements:
• To get N_A hydrogen molecules, we must take 2 grams of hydrogen atoms 
• To get N_A oxygen molecules, we must take 32 grams of oxygen atoms 
• To get N_A ozone molecules, we must take 48 grams of oxygen atoms
• To get N_A sulphur molecules, we must take 256 grams of sulphur atoms 
• To get N_A helium molecules, we must take 4 grams of helium atoms
■ Molecules of compounds
• To get N_A water molecules, we must take 18 grams of water
• To get N_A carbon dioxide molecules, we must take 44 grams of carbon dioxide
• To get N_A glucose molecules, we must take 180 grams of glucose

---

Is there an easier method to get the above masses? Let us try:

■ Consider a molecule of hydrogen. 
1. The molecule is H₂. It has two hydrogen atoms. 
2. So total mass of a molecule of hydrogen will be twice the mass of a hydrogen atom
3. We know that, the mass of a hydrogen atom is 1 u
4. So mass of a hydrogen molecule = (2 × 1 u) = 2 u
5. Above we found that, to get N_A hydrogen molecules, we must take 2 grams of hydrogen atoms   
• In (4) we have 2 u. 
• In (5) we have 2 grams
• The numeric parts are the same 

■ Consider a molecule of oxygen. 
1. The molecule is O₂. It has two oxygen atoms. 
2. So total mass of a molecule of oxygen will be twice the mass of a oxygen atom
3. We know that, the mass of a oxygen atom is 16 u
4. So mass of a oxygen molecule = (2 × 16 u) = 32 u
5. Above we found that, to get N_A oxygen molecules, we must take 32 grams of oxygen atoms   
• In (4) we have 32 u. 
• In (5) we have 32 grams
• The numeric parts are the same

■ Consider a molecule of ozone. 
1. The molecule is O₃. It has three oxygen atoms. 
2. So total mass of a molecule of ozone will be thrice the mass of a oxygen atom
3. We know that, the mass of a oxygen atom is 16 u
4. So mass of a ozone molecule = (3 × 16 u) = 48 u
5. Above we found that, to get N_A ozone molecules, we must take 48 grams of oxygen atoms   
• In (4) we have 48 u. 
• In (5) we have 48 grams
• The numeric parts are the same

■ Consider a molecule of sulphur. 
1. The molecule is S₈. It has eight sulphur atoms. 
2. So total mass of a molecule of sulphur will be eight times the mass of a sulphur atom
3. We know that, the mass of a sulphur atom is 32 u
4. So mass of a sulphur molecule = (8 × 32 u) = 256 u
5. Above we found that, to get N_A sulphur molecules, we must take 256 grams of sulphur atoms   
• In (4) we have 256 u. 
• In (5) we have 256 grams
• The numeric parts are the same

■ Consider a molecule of helium. 
1. The molecule is H. It has only one helium atom. 
2. So total mass of a molecule of helium will be same as the mass of a helium atom
3. We know that, the mass of a helium atom is 4 u
4. So mass of a helium molecule = (1 × 4 u) = 4 u
5. Above we found that, to get N_A helium molecules, we must take 4 grams of helium atoms   
• In (4) we have 4 u. 
• In (5) we have 4 grams
• The numeric parts are the same

■ Consider a molecule of water. 
1. The molecule is H₂O. It has two hydrogen atoms and one oxygen atom. 
2. So total mass of a molecule of water will be the sum of:
• twice the mass of a hydrogen atom
• mass of  an oxygen atom
3. We know that, the mass of a hydrogen atom is 1 u and that of oxygen atom is 16 u
4. So mass of a water molecule = (2 × 1 u) + (1 × 16 u)   = 2 u + 16 u = 18 u
5. Above we found that, to get N_A water molecules, we must take 18 grams of water 
• In (4) we have 18 u. 
• In (5) we have 18 grams
• The numeric parts are the same

■ Consider a molecule of carbon dioxide. 
1. The molecule is CO₂. It has one carbon atom and two oxygen atoms. 
2. So total mass of a molecule of carbon dioxide will be the sum of:
• mass of a carbon atom
• twice the mass of an oxygen atom
3. We know that, the mass of a carbon atom is 12 u and that of oxygen atom is 16 u
4. So mass of a carbon dioxide molecule = (1 × 12 u) + (2 × 16 u)   = 12 u + 32 u = 44 u
5. Above we found that, to get N_A carbon dioxide molecules, we must take 44 grams of carbon dioxide
• In (4) we have 44 u. 
• In (5) we have 44 grams
• The numeric parts are the same

■ Consider a molecule of glucose. 
1. The molecule is C₆H₁₂O₆. It has six carbon atoms, twelve hydrogen atoms and six oxygen atoms. 
2. So total mass of a molecule of glucose will be the sum of:
• six times the mass of a carbon atom
• twelve times the mass of a hydrogen atom
• six times the mass of an oxygen atom
3. We know that, the mass of a carbon atom is 12 u, mass of a hydrogen atom is 1 u and that of an oxygen atom is 16 u
4. So mass of a glucose molecule = (6 × 12 u) + (12 × 1 u) + (6 × 16 u) = 72 u + 12 u + 96 u = 180 u
5. Above we found that, to get N_A glucose molecules, we must take 180 grams of glucose
• In (4) we have 180 u. 
• In (5) we have 180 grams
• The numeric parts are the same

---

So we can write:

• Each molecule (it may be 'a molecule of an element' or 'a molecule of a compound') will have a unique value for the 'mass in grams' 

• If we take that much mass of that element/compound, there will be N_A number of molecules

• This unique mass is called 'Gram Molecular Mass' (GMM) of that molecule
Some examples:
• GMM of element oxygen is 16 grams
    ♦ In 16 grams of oxygen, there will be N_A molecules of oxygen
• GMM of element helium is 4 grams
    ♦ In 4 grams of helium, there will be N_A molecules of helium
• GMM of compound glucose is 180 grams
    ♦ In 180 grams of glucose, there will be N_A molecules of glucose

---

The GMM of any molecule can be written using the following steps

Step 1: Calculate the total mass of one molecule. It's unit will be in 'u'
Step 2: Write the numeric part
Step 3: Write 'grams' on the right side
This will give the GMM of that molecule

---

Some examples:

1. Find the GMM of ammonia (NH₃)
Solution:
Step 1: Total mass of one molecule:
Mass of one nitrogen atom = 14 u
Mass of one hydrogen atom = 1 u
So total mass = (1 × 14 u) + (3 × 1 u) = 14 u + 3 u = 17 u
Step 2: Write the numeric part: 17
Step 3: Write 'grams' on the right side. We get: 17 grams
So GMM of ammonia is 17 grams

1. Find the GMM of HCl
Solution:
Step 1: Total mass of one molecule:
Mass of one hydrogen atom = 1 u
Mass of one chlorine atom = 35.5 u
So total mass = (1 × 1 u) + (1 × 35.5 u) = 1 u + 35.5 u = 36.5 u
Step 2: Write the numeric part: 36.5
Step 3: Write 'grams' on the right side. We get: 36.5 grams
So GMM of ammonia is 36.5 grams

---

Once we understand the basics, there will not be any need to write the steps. Just write the total mass of one molecule, and write 'grams' instead of 'u'

We will now see some solved examples

Solved example 10.1
How many water molecules are present in 90 grams of water?
Solution:
1. GMM of water (H₂O) = (2 × 1) + (1 × 16) = 2 + 16 = 18 grams
2. No. of GMMs in 90 grams of water = ⁹⁰⁄₁₈  = 5
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 5 GMMs = 5N_A = 5 × 6.022×10²³

---

Let us do the above problem by another method, which uses some very basic information:

1. We have:
No. of molecules ×  Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 90 grams
3. Mass (in u) of one molecule of water = (2 × 1) + (1 × 16) = 2 + 16 = 18 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 18 u = 18 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 5 × 6.022×10²³ that we got earlier.  
In these types of problems, it is worthy to always remember that, the reciprocal of 'u in grams' gives the Avogadro number N_A. That is:      

We can check it using a calculator

---

Solved example 10.2

Samples of some compounds are given:
(i) 85 grams of ammonia (NH₃) 
(ii) 90 grams of glucose (C₆H₁₂O₆)
(iii) 88 grams of carbon dioxide (CO₂)
(iv) 50 grams of hydrogen (H₂)  
• Find the number of molecules in each sample. (Hint: GAMs are: H = 1g, C = 12 g, N = 14 g, O = 16 g)
Solution (i):
1. GMM of ammonia (NH₃) = (1 × 14) + (1 × 3) = 14 + 3 = 17 grams
Note: For this step we require the atomic masses (in u) of nitrogen and hydrogen. But they are given to us in the form of GAM. We know that, GAM is numerically same as u. 
2. No. of GMMs in 85 grams of water = ⁸⁵⁄₁₇  = 5
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 5 GMMs = 5N_A = 5 × 6.022×10²³

---

Let us do the problem by another method, which uses some very basic information:

1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 85 grams
3. Mass (in u) of one molecule of water = (1 × 14) + (1 × 3) = 14 + 3 = 17 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 18 u = 18 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 5 × 6.022×10²³ that we got earlier.

Solution (ii):
1. GMM of glucose (C₆H₁₂O₆) = (6 × 12) + (1 × 12) + (6 × 16) = 72 + 12 + 96 = 180 grams
2. No. of GMMs in 90 grams of water = ⁹⁰⁄₁₈₀  = 0.5
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 0.5 GMMs = 0.5N_A = 0.5 × 6.022×10²³

---

Let us do the above problem by the other method:

1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 90 grams
3. Mass (in u) of one molecule of glucose = (6 × 12) + (1 × 12) + (6 × 16) = 72 + 12 + 96 = 180 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 180 u = 180 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 0.5 × 6.022×10²³ that we got earlier.  

Solution (iii):
1. GMM of carbon dioxide (CO₂) = (1 × 12) + (16 × 2) = 12 + 32 = 44 grams
2. No. of GMMs in 88 grams of water = ⁸⁸⁄₄₄  = 2
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 2 GMMs = 2N_A = 2 × 6.022×10²³

---

Let us do the above problem by the other method:

1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 88 grams
3. Mass (in u) of one molecule of carbon dioxide = (1 × 12) + (16 × 2) = 12 + 32 = 44 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 44 u = 44 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 2 × 6.022×10²³ that we got earlier.

Solution (iv):
1. GMM of hydrogen (H₂) = (2 × 1) = 2 grams
2. No. of GMMs in 50 grams of water = ⁵⁰⁄₂  = 25
3. 1 GMM will contain N_A molecules. 
4. So no. of molecules in 25 GMMs = 25N_A = 25 × 6.022×10²³

---

Let us do the above problem by the other method:

1. We have:
No. of molecules × Mass (in grams) of one molecule = Given total Mass (in grams)
⇒ No. of molecules = ^{Given total Mass (in grams)}⁄_{Mass (in grams) of one molecule}.  
2. Given total mass = 50 grams
3. Mass (in u) of one molecule of glucose = (2 × 1) = 2 u
4. But 1 u = 1.6605×10^-24 grams  (Details here)
So 2 u = 2 × 1.6605×10^-24 grams
5. Substituting this value in (1) we get:

■ We get the same result 2 × 6.022×10²³ that we got earlier.

---

Based on the above discussion, we can now take up 'mole'. We will see it in the next section. 

PREVIOUS      CONTENTS       NEXT

                        Copyright©2017 High school Chemistry lessons. blogspot.in - All Rights Reserved